Combinatória - Márcia R. Cerioli

Diagramas de Venn

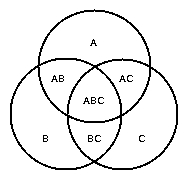Um diagrama de Venn para n conjuntos consiste basicamente
de n curvas simples e fechadas no plano que determinam uma região conexa
para cada uma das interseções que os conjuntos formam.

Diagramas de Venn sempre existem.

Diagramas de Venn sempre existem para todos os valores de n.
São conhecidas várias construções gerais, das quais duas são descritas abaixo:

(a) Construção de Venn

A construção de Venn descrita em seu artigo original (1880) é melhor explicada considerando a figura à direita. Comece com o diagrama usual com 3 círculos. Curvas são sucessivamente acrescentadas, com a nova curva sendo traçada sobre a última acrescentada e dobrando o número de regiões. Na figura, elas são acrescentadas na ordem azul (4), vermelha (5) e verde (6). A sétima curva deverá ser acrescentada da mesma maneira.

(b) Construção de Edwards

Anthony Edwards (1989) desenvolveu outra construção indutiva geral que tem muitas propriedades interessantes, incluindo alguma simetria. Também será descrita por meio de um exemplo, no diagrama à esquerda. Para n=2 o diagrama consiste de duas linhas perpendiculares. (Na verdade, deveríamos ligar os extremos destas linhas de modo a obter linhas fechadas.) Para n=3 um círculo é acrescentado. Curvas subseqüentes serão todas acrescentadas seguindo este círculo, indo sinuosamente para dentro e fora do círculo. Novamente dobrando o número de regiões. Para n=4,5,6 as curvas azul, vermelha e verde são acrescentadas, nesta ordem.

Clique aqui para ver uma animação desta construção.

E se as figuras devem ser todas do mesmo tipo?

Aí já não é sempre o caso que diagramas de Venn sempre existem. Por exemplo, se as figuras são círculos, só é possível fazer o diagrama para n=1,2 e 3. Quatro círculos definem no máximo 14 regiões.
Já se as figuras são retângulos, existem construções para n=1,2,3, 4 e 5. Mas ainda esta em aberto se existe um diagrama de Venn formado por 6 retângulos.
A construção com 5 retângulos é devida a Boyd (1985) e pode ser encontrada em Mathematic Magazine vol. 58, pagina 251.
Página elaborada em 24 abr 04 por Márcia R. Cerioli